Computación cuántica en la nube

[Published originally in Revista Española de Física Vol 34, No 1 (2020).]

La idea de codificar información en sistemas cuánticos y procesar ésta de una manera más eficiente mediante el aprovechamiento de propiedades como la superposición y el entrelazamiento se remonta a la década de 1980. El campo de la computación cuántica se mantuvo en un ámbito casi exclusivamente académico hasta la década de 2010, momento en el cual grandes empresas comienzan a participar activamente en el desarrollo de ordenadores cuánticos. En contraste con otras revoluciones tecnológicas, el desarrollo de la computación cuántica se está caracterizando por una estrecha colaboración entre el mundo académico y el empresarial, en la cual las compañías han dado libre acceso a sus plataformas a los investigadores y promueven el desarrollo abierto de nuevas ideas mediante la enseñanza y la organización de concursos.

Introducción

Hace aproximadamente ciento veinte años descubrimos una de las teorías física más bellas y fundamentales de la naturaleza: la mecánica cuántica. Durante la primera mitad del siglo XX, los esfuerzos se centraron en la formalización de la teoría, y a partir de los años cincuenta, las aplicaciones comenzaron a surgir. El desarrollo de dispositivos como el transistor, el láser, el GPS o la resonancia magnética marcaron el inicio de lo que ahora conocemos como la primera revolución cuántica. Aprendimos a aplicar los fenómenos cuánticos colectivos para mejorar nuestro día a día. Ahora, setenta años después, la segunda revolución cuántica es posible gracias a los numerosos avances en el control de sistemas cuánticos individuales, que permiten explotar fenómenos como la superposición, el entrelazamiento y la interferencia. Esto supone tener a nuestra disposición todos los recursos que nos proporciona la mecánica cuántica para realizar medidas más sensibles, computaciones más sofisticadas o comunicaciones más seguras.

En los últimos años, un gran número de instituciones han puesto en marcha programas para habilitar el desarrollo teórico, experimental e industrial de dispositivos cuánticos. Con el ánimo de impulsar esta revolución, la Unión Europea ha lanzado el programa Quantum Flagship [1]: 1000 millones de euros para que las tecnologías cuánticas sean una realidad antes de 2028. El Quantum Flagship se basa en cuatro pilares fundamentales donde se espera que las tecnologías cuánticas tengan un gran impacto a corto y medio plazo: comunicación, computación, simulación y metrología. En este artículo nos vamos a centrar en una de ellas, la computación cuántica, que permite realizar cálculos que pueden llegar a ser prohibitivamente costosos en ordenadores clásicos.

La carrera por el ordenador cuántico

La computación cuántica utiliza las propiedades que esta teoría física nos brinda para realizar cálculos de un modo totalmente diferente a la de los ordenadores convencionales. Esto supone un nuevo paradigma en la computación, pues dichas propiedades hacen replantearnos el modo en que diseñamos los algoritmos. Los ladrillos de esta nueva computación son los bits cuánticos, comúnmente llamados qubits. Del mismo modo que en computación clásica usamos los transistores para generar los bits, hemos de buscar sistemas cuánticos que funcionen como qubits. Estos deben ser sistemas de dos niveles bien definidos (el del 0 y el del 1) que puedan interactuar entre sí conservando las propiedades cuánticas que les hacen característicos. Y es que una de las principales ventajas de la computación cuántica es la capacidad de los qubits de hallarse en una superposición de estados coherente que permite, entre otras cosas, aplicar una misma operación a todos los elementos de dicha superposición simultáneamente. Si a todo ello le añadimos entrelazamiento entre los qubits y la posibilidad de interferencia, generamos una serie de correlaciones sofisticadas imposibles de reproducir clásicamente.

A pesar del gran reto tecnológico que implica la fabricación de estos dispositivos, los ordenadores cuánticos son ya una realidad. Muchos grupos de investigación de todo el mundo hace años que tienen pequeños prototipos. Pero, sin duda, este campo ha experimentado una gran expansión cuando compañías privadas han decidido apostar por él. En 2010, IBM decidió tomar la delantera y empezar a desarrollar prototipos experimentales. Su anuncio salió tres años después que la compañía canadiense D-Wave asegurara tener un chip cuántico de 16 qubits. Aunque el tipo de computación que realiza D-Wave no es universal y consecuentemente sus qubits son muy diferentes a los de IBM y otras compañías, este anuncio probablemente dio el pistoletazo de salida a la carrera cuántica empresarial. Después de IBM, otras compañías se sumaron a esta carrera: Google, Intel, Microsoft, Alibaba,… además de crearse nuevas empresas salidas directamente de aquellas universidades que llevaban años en el campo. Un ejemplo es Rigetti Computing, nacida en la Universidad de Yale y ahora una de las principales competidoras en el área. A nivel local, otro ejemplo es Qilimanjaro, una empresa recién creada en Barcelona cuyo objetivo es construir el primer ordenador cuántico del sur de Europa.

¿Quién será el primero que demuestre una ventaja cuántica? Es decir, ¿quién podrá correr un algoritmo o una simulación imposible de realizar por un ordenador clásico? El límite de la ventaja cuántica varía con la mejora de los superordenadores clásicos y con el desarrollo de nuevos métodos para simular sistemas cuánticos. Aun así, en el mejor de los casos, un ordenador clásico no será capaz de gestionar suficiente memoria como para simular más de 100 qubits. Los prototipos más grandes de ordenadores cuánticos de hoy en día están formados por 50 qubits (IBM), 72 qubits (Google) y 128 qubits (en proceso de construcción por Rigetti). Todo apunta a que estamos muy cerca de alcanzar la ventaja cuántica.

Sin embargo, todos los dispositivos mencionados siguen siendo prototipos debido a que son “ruidosos”. Para realizar un algoritmo cuántico correctamente es necesario que los qubits mantengan la coherencia y que las puertas lógicas cuánticas se implementen de forma perfecta. Esto es experimentalmente muy difícil, por lo que se asume que se van a necesitar códigos de corrección de errores cuánticos. Dichos códigos necesitan del orden de 100 qubits para corregir el estado de uno solo, lo que hace materialmente imposible, a día de hoy, tener un ordenador cuántico sin fuentes de error. Por todo ello, se ha bautizado a esta primera fase de la computación cuántica como NISQ [2] (Noisy Intermediate-Scale Quantum computation), en contraposición a la Fault-tolerant Quantum computation , que nos permitirá trabajar con qubits perfectos (llamados “lógicos”). Cabe mencionar otras propuestas de algoritmos cuánticos que, en principio, no necesitan corregir errores. Son llamados algoritmos variacionales o híbridos , por usar tanto computación cuántica como clásica para sortear el problema del ruido.

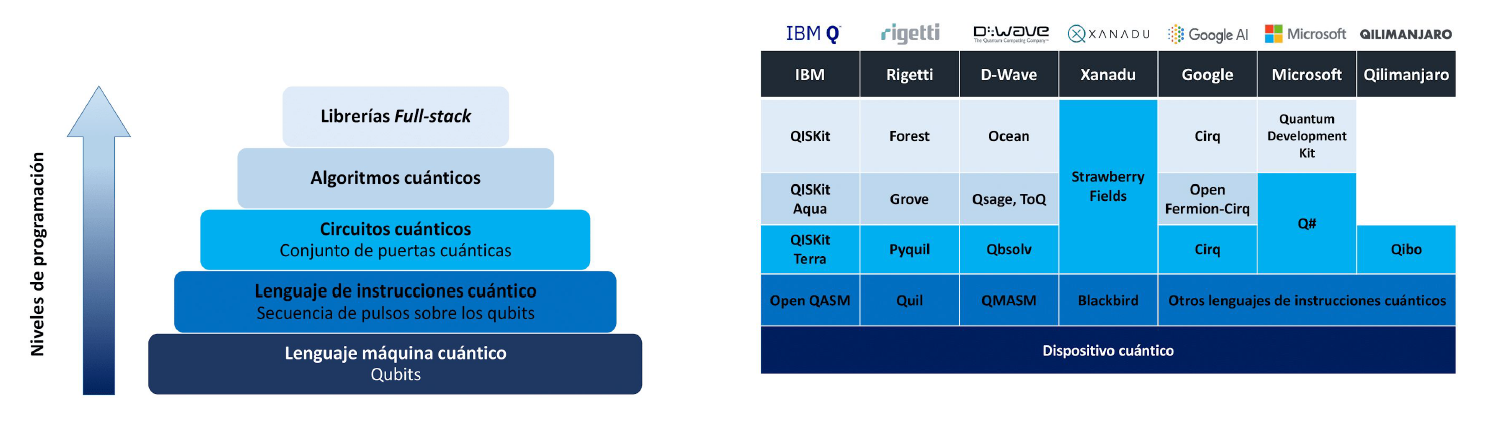
En esta carrera para alcanzar la ventaja cuántica, las empresas privadas se han dado cuenta que la colaboración de todos va a ser fundamental. Al fin y al cabo, la computación cuántica es un campo relativamente nuevo y los conocimientos necesarios para pensar e implementar algoritmos cuánticos se enseñan casi exclusivamente en las universidades. Por este motivo, algunas compañías ofrecen acceso a sus ordenadores cuánticos de forma gratuita a través de internet. Cada empresa está desarrollando su propio lenguaje de programación para enviar instrucciones a su chip cuántico de modo que no sea necesario tener el ordenador enfrente [3,4]. Cualquier persona puede instalarse estos lenguajes (normalmente en forma de “packages” de algún lenguaje conocido como Python), programar su conjunto de instrucciones cuánticas en su portátil y ejecutar el programa en la nube. Éste es corrido en el chip cuántico en cuestión y los resultados son enviados al usuario para que los procese y analice como desee. El sueño de muchos científicos teóricos se hace realidad: tener acceso directo al experimento desde el despacho.

El pasado año, la empresa IBM convocó una serie de cuatro premios con el objetivo de fomentar el uso de sus dispositivos cuánticos y explorar sus posibles aplicaciones. El premio “Teach Me QISKit” se otorgó al mejor algoritmo cuántico programado en su lenguaje de programación que demostrara alguna aplicación interesante en forma de tutorial. El premio “Best Paper” se otorgó a las mejores publicaciones científicas que hicieran uso de alguno de sus ordenadores cuánticos. El premio “Teach Me Quantum” se otorgó al mejor material para realizar un curso introductorio en computación cuántica y el premio “QISKit Developer Challenge” al mejor compilador cuántico. Los autores del presente artículo fueron galardonados con los dos primeros. En las siguientes secciones, presentamos un resumen de nuestros trabajos, que a la vez sirven de ejemplo de uso y aplicaciones de un ordenador cuántico.

Transición de fase cuántica en un ordenador cuántico

Una de las primeras personas en proponer la construcción de un ordenador cuántico fue el gran físico Richard Feynman. En su artículo de 1982 “Simulando la física con ordenadores” [5], puso de manifiesto el coste exponencial de la simulación de sistemas cuánticos. Feynman planteó ¿por qué no construir un ordenador, las piezas del cual se comporten de forma cuántica también? Eso simplificaría enormemente el coste computacional, pues cada uno de los qubits de este ordenador podría albergar el estado de una partícula, y la interacción entre ellos podría describir una interacción real de un sistema cuántico. La primera aplicación de un ordenador cuántico es, precisamente, la simulación cuántica. Desde su propuesta hace más de un siglo, el modelo de Ising ha sido usado como modelo simplificado para explicar el magnetismo a nivel microscópico. Además de su versión clásica, existe el modelo de Ising cuántico, el cual presenta una transición de fase en una dimensión cuando se considera un campo externo transversal. Esta transición es cuántica, es decir, el estado fundamental pasa de ser paramagnético a ferromagnético por fluctuaciones cuánticas, a temperatura cero.

Es posible encontrar un circuito cuántico que simule de forma exacta el modelo de Ising. Podemos entonces simular con un ordenador cuántico las características más importantes de este modelo, en especial su transición de fase cuántica. El circuito cuántico en cuestión nos da acceso no solo al estado fundamental sino también a cualquier estado del espectro de Ising. Esto implica la posibilidad de simular la evolución temporal o estados térmicos, elementos de especial interés en el campo de la física de la materia condensada. Además, el modelo de Ising en una dimensión es integrable, es decir, podemos obtener el espectro de energías y estados cuánticos analíticamente. Con ello, podemos comparar los resultados obtenidos con el ordenador cuántico con las expresiones teóricas y así comprobar cómo de bueno es el ordenador.

Como hemos dicho anteriormente, los ordenadores cuánticos de hoy en día están compuestos de pocos qubits. Sin embargo, esto no supone una barrera para ejecutar pequeños experimentos y ver así cómo se comportan. Podemos entonces construir un pequeño circuito cuántico que simule el modelo de Ising para una cadena de cuatro espines, usando un qubit para representar el estado de cada uno de ellos. Este circuito se puede enviar a los ordenadores cuánticos como los que ofrecen en la nube IBM o Rigetti Computing. El resultado de dicho experimento se presenta en la Figura 3, donde se muestra el valor esperado del campo magnético en función del campo transversal λ . A medida que dicho campo aumenta, los espines tienden a alinearse hasta que sucede la transición de fase cuántica y se produce un salto en la magnetización. El lector interesado puede consultar la referencia [6] y encontrar el tutorial para implementar este algoritmo cuántico y otros en [3].

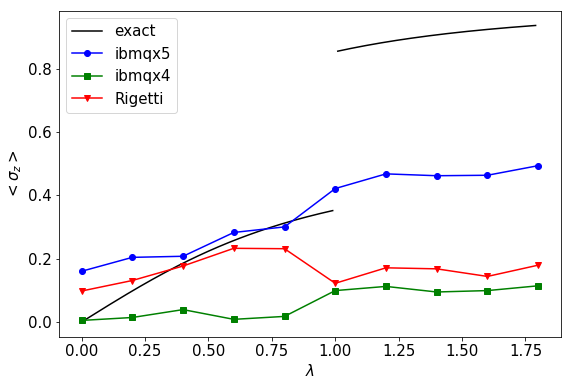
Aunque el resultado pueda parecer descorazonador al alejarse tanto de la predicción exacta, pueden encontrarse varias explicaciones. Primero, los qubits son “ruidosos”, es decir, varios factores pueden provocar que cada uno de ellos no se encuentre en el estado que le tocaría al terminar el algoritmo. La coherencia cuántica de los qubits es fundamental en este tipo de computación. Sólo si éstos se encuentran en un estado coherente, sus propiedades cuánticas pueden ser explotadas para la realización correcta del algoritmo. El tiempo de coherencia es limitado, lo que nos da un cierto margen de tiempo para implementar todas las puertas lógicas necesarias antes de terminar la computación. Si nos pasamos de ese tiempo, todo lo que hagamos no tendrá el efecto deseado, provocando numerosos errores.

En segundo lugar, las puertas lógicas cuánticas son operaciones físicas que hay que programar de un modo muy preciso y que dependen de las características físicas de cada qubit. Hay todo un sistema de control cuántico de estas puertas que debe ser sumamente sofisticado y las limitaciones experimentales nos impiden estar libres de errores. Éstos se van propagando a medida que aplicamos más y más puertas. Ambos factores se corregirán en un futuro cuando sea posible aplicar códigos de corrección de errores a nuestros ordenadores cuánticos.

El hecho de que podamos observar el comportamiento de un sistema cuántico real, a pesar de todas estas fuentes de error y de la gran dificultad técnica que entraña el control de sistemas cuánticos individuales, es un salto tecnológico muy importante. Experimentos como éste son pruebas de concepto, es decir, pequeñas demostraciones de nuestro poder experimental que sientan las bases de lo que seremos capaces de hacer.

Computación cuántica para inteligencia artificial

Otro ámbito en el cual se espera que el uso de ordenadores cuánticos presente un gran avance con respecto al uso ordenadores tradicionales es en el aprendizaje automático o machine learning . Actualmente, los algoritmos de aprendizaje automático se encargan de manejar y analizar cantidades ingentes de datos para encontrar patrones a través de los cuales nueva información pueda ser clasificada, predicha, o generada. A día de hoy, los algoritmos de machine learning están detrás de las recomendaciones de Amazon y Netflix, de los sistemas de control de coches autónomos, o de los aparatos de reconocimiento facial de los aeropuertos. El mundo de la investigación no se ha quedado atrás, y recientemente el aprendizaje autónomo ha sido noticia en áreas tan diversas como el reconocimiento temprano de enfermedades o en el descubrimiento de exoplanetas.

La principal característica de la mayoría de los algoritmos utilizados actualmente (conocidos como algoritmos de deep learning o aprendizaje profundo) es la gran cantidad de parámetros utilizados para modelar el conjunto de datos estudiado. Esto hace que sea muy complicado conocer cuál es la característica específica que determina la predicción, siendo estos algoritmos tratados como cajas negras que solamente arrojan resultados, sin explicaciones. Además, los métodos de entrenamiento de dichos algoritmos dificultan la obtención de información adicional a la de la predicción en sí. Esto hace que preguntas como “¿cuán seguro se está de que la predicción realizada es la correcta?” o “¿cuál es la diferencia de confianza entre la primera y la segunda opción?” sean muy complicadas de responder. Dado que se espera que en los próximos años estos algoritmos tengan cada vez más y más relevancia en nuestras vidas, es importante desarrollar herramientas que nos permitan “abrir la caja” y obtener información acerca del proceso de predicción [7].

Una de las maneras de obtener más información acerca de los funcionamientos internos de los algoritmos es el cambio de paradigma en el entrenamiento, transitando del cálculo y la optimización de funciones a la teoría de la probabilidad y el teorema de Bayes. En este paradigma, el objeto central no es la predicción en sí, sino la distribución de probabilidad de predicciones condicionada en el conjunto de datos de entrenamiento. Esto permite que preguntas como las planteadas anteriormente sean fáciles de responder.

Sin embargo, las técnicas de entrenamiento Bayesiano de algoritmos de aprendizaje automático tienen un alto coste computacional. Es justo aquí donde la computación cuántica resulta una gran aliada. Suponiendo que uno pueda codificar de manera eficiente la información a analizar en sistemas cuánticos, es posible aprovechar la superposición cuántica para reducir drásticamente los costes computacionales.

El problema de resolver sistemas lineales de ecuaciones es un claro ejemplo donde la computación cuántica puede ofrecer una ventaja. Dados una matriz de coeficientes $A$ y un vector de valores $b$, el problema consiste en obtener el vector solución $x$ que cumple $Ax = b$. La resolución de este problema viene dada por $x = A^{−1}b$ , lo cual necesita del cálculo de la inversa de la matriz $A$. Si esta matriz tiene dimensión $n$, son necesarias del orden de $n^{3}$ operaciones para calcular su inversa. Sin embargo, en caso de poder crear un sistema cuántico en el estado $|b\rangle$ y un operador cuyos coeficientes vengan determinados por la matriz A , existe un algoritmo cuántico que permite evolucionar el sistema hacia el estado $|x\rangle= A^{−1}|b\rangle$ realizando del orden de $\log(n)$ operaciones [8].

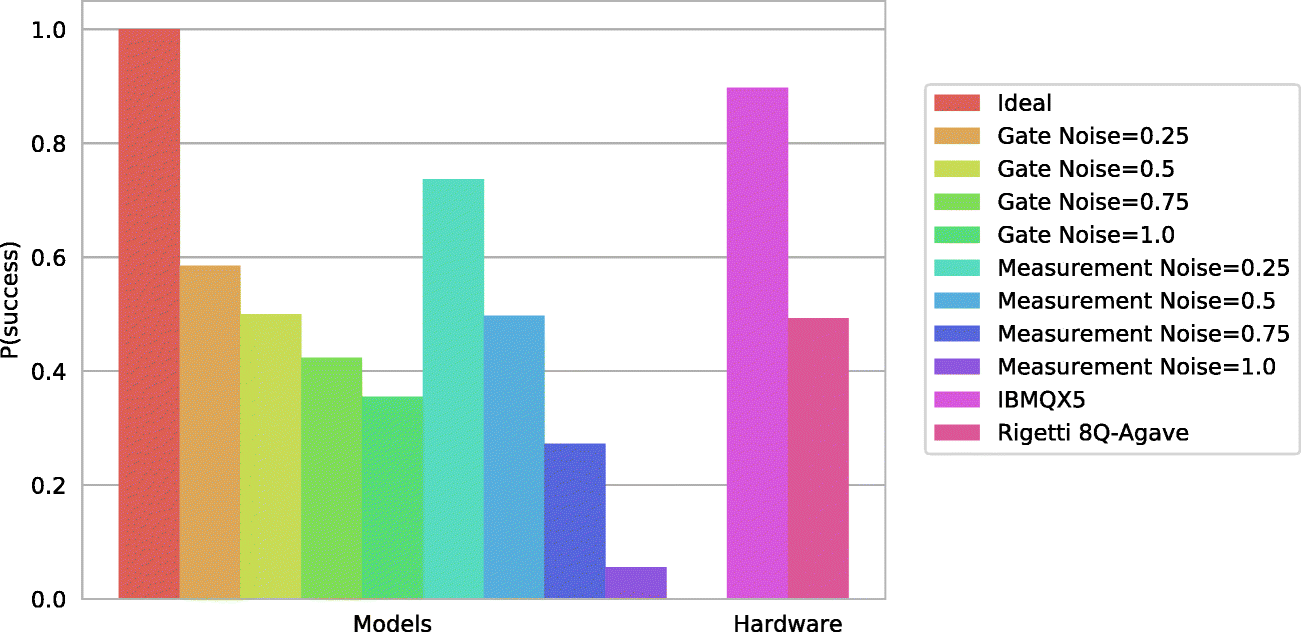
Con esta motivación, en [9] se desarrolló un algoritmo cuántico para llevar a cabo entrenamiento de redes neuronales utilizando una técnica Bayesiana denominada “Procesos Gaussianos” . Dicha técnica requiere de la inversión de matrices que son de un tamaño comparable a la cantidad de datos a estudiar. En el caso de aplicaciones en aprendizaje profundo, el coste computacional de esta operación es prohibitivo en ordenadores clásicos. Como parte del proyecto, se estudió cuán factible es la inversión de matrices en los ordenadores cuánticos actuales de las compañías IBM y Rigetti Computing. Pronto fueron patentes los dos problemas más acusados de los ordenadores NISQ. Por un lado, la limitada conectividad entre qubits provoca que en muchas ocasiones sea necesario reservar algunos para cálculos intermedios, de modo que no se puedan resolver problemas muy grandes. Por otro lado, el corto tiempo de coherencia de los qubits, comentado anteriormente, aleja el resultado final del esperado. A pesar de esto, se observó que para el caso de inversión de pequeñas matrices, los ordenadores de IBM consiguen preparar estados razonablemente satisfactorios. El lector interesado que quiera probar los programas ejecutados en dicho estudio desde su casa, experimentar o incluso sugerir mejoras, puede encontrarlos en [10].

Ciencia abierta y colaborativa

A pesar de los desafíos experimentales que conlleva la computación cuántica, los ordenadores cuánticos han llegado para quedarse. Estamos viviendo una revolución tecnológica como lo fue en su día el desarrollo de la computación clásica. El ordenador cuántico es una nueva herramienta de cálculo que promete aplicaciones en gran variedad de ámbitos: química, finanzas, machine learning, ciencia de materiales, etc. Una vez más, la ciencia avanza más rápido gracias a las grandes colaboraciones. La computación cuántica ya no es patrimonio único de los físicos. Arquitectos de sistemas, desarrolladores de software, e ingenieros electrónicos entre muchas otras profesiones, son necesarios para abandonar los prototipos y construir un ordenador cuántico universal. Del mismo modo, son necesarios investigadores de áreas tan diversas como sea posible, para así explorar qué problemas pueden hallar la solución en el uso de la mecánica cuántica. Desde aquí, nos gustaría hacer un llamamiento a la ciencia abierta, que pone a la libre disposición de los usuarios e investigadores los avances científicos más punteros. Los retos tecnológicos que plantean las tecnologías cuánticas en general, y la computación cuántica en particular, exigen un gran esfuerzo colaborativo que será sobradamente compensado con las aplicaciones que nos ofrece esta nueva revolución.

Referencias

[1] Quantum Flagship webpage.
[2] J. Preskill (2018), “Quantum Computing in the NISQ era and beyond”. Quantum 2, 79.
[3] IBMQ, Quantum Instruction Set.
[4] Rigetti Computing full-stack library.
[5] R. P. Feynman (1982), “Simulating physics with computers”. International Journal of Theoretical Physics 21, 467- 488.
[6] A. Cervera-Lierta (2018), “Exact Ising model simulation on a quantum computer”. Quantum 2, 114.
[7] Guía ética para una IA confiable.
[8] A. W. Harrow, A. Hassidim, S. Lloyd (2008). “Quantum algorithm for solving linear systems of equations”. Physical Review Letters 103 (15), 150502, arXiv:0811.3171 [quant-ph].
[9] Z. Zhao, A. Pozas-Kerstjens, P. Rebentrost, P. Wittek (2019). “Bayesian Deep Learning on a Quantum Computer”. Quantum Machine Intelligence 1, 1-11.
[10] Repositorio bayesian-dl-quantum.