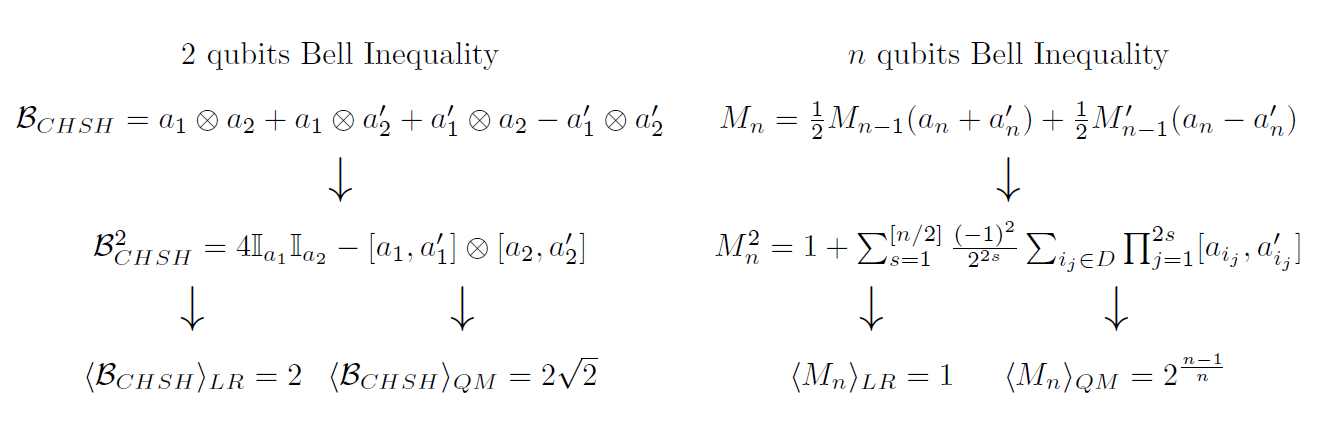How I became a quantum computation scientist

[Originally posted in Qiskit Medium page]

Oxford, May 5th of 2016. As every morning since I started my scholarship 4 months before, I woke up, took my old borrowed bicycle (that almost killed me several times) and rode across Oxford city, from Raleigh Park to Keble Road, the site for Particle Theory group of Rudolph Pierls Institute for Theoretical Physics. My daily routine upon arriving at my office began with a glass of water, which I drank while reading the news, followed by a coffee, which I enjoyed while reading quant-ph and hep-th on arXiv. That day I stumbled upon an amazing piece of news. IBM had announced an “advanced quantum processor to not just the scientific community, but the general public, providing access to a quantum computing platform from any desktop or mobile device via the cloud”. Immediately, I sent an email to my group in Barcelona. Of course, they had read the news as well, they were already registered in IBM Quantum Experience and had some ideas…

We had been working on Bell Inequalities since I started my Ph.D. 8 months before, concretely those for more than two qubits, known as Mermin inequalities, and new proposals for qutrits. Since IBM offered a quantum computer of 5 qubits, they decided to check if these inequalities are violated. In other words, was that quantum device actually quantum? Daniel Alsina, at that time a Ph.D. student, told me later that he and our advisor closed themselves in their office until they programmed all needed circuits. No sooner said than done, on May 13th of 2016 I received an email with their work published on arXiv. The first paper using IBM quantum computer proved the violation of Mermin inequalities. That device was truly quantum!

To my mind that was a milestone in my Ph.D. and probably in my career. It was the first year of my Ph.D., I had done some work on Bell Inequalities and I was starting the central work of my Ph.D. thesis, entanglement in particle physics. But the creation of a public quantum computing platform to run real experiments on the cloud opened a new path. “Does it work properly?” “Is it big enough to program a quantum algorithm?” “What kind of algorithms can we design in that device?” “Could it be useful in the short-term?” These are some of the questions that came into my mind and very likely to other members of the quantum computing community as well, specially theoreticians. Cloud computation brought us closer to the experiment; we could design and test our algorithms and check if they work in near-term quantum computers.

When I came back from Oxford, I continued working on entanglement in particle physics but I also started to learn how to use a quantum computer. Last year, our group in the University of Barcelona joined forces with Barcelona Supercomputing Center and started a new group on quantum computation. We, Quantic, aim at building a quantum computer in the Barcelona area. This new project brings me even closer to the experiment, which is enticing. The experimental team has just started to set up the laboratory and we, the theoreticians, continue working with the usual tools, namely paper, pen and laptop, together with remote quantum devices that we can run on the cloud.

IBM “Teach Me QISKit” award

I love a Spanish popular idiom that translates literally as “the devil is wiser for being old than for being the devil”. That is, there’s no substitute for experience. A lot of work has been done in quantum computation since the field started in the ’80s. Many generations of theoretical physicists have proposed and improved quantum algorithms, but most of them have not been tested in real devices. It is a good moment to check the literature and push these works into the open.

An article came to my hands as a recommendation from my advisor: “Quantum Circuits for Strongly Correlated Quantum Systems”, by Frank Verstraete, Juan Ignacio Cirac and José Ignacio Latorre. They proposed a quantum algorithm which diagonalizes exactly certain kind of Hamiltonians, in particular de XY Hamiltonian. That circuit mapped the computational basis states into the eigenstates of the Hamiltonian. By preparing initial qubits in a product state one obtains the ground or excited states. They provided an example of this circuit for n=4 and n=8 spins using one and two-qubit gates, but the needed operations are not part of the basic sets in current quantum devices.

I decided to adapt this circuit for the Ising model Hamiltonian, a particular case of XY model, using the quantum gates available in the experiments. Once I had this circuit programmed, I could do several experiments. The one-dimensional Ising model is one of the most simple models to describe an interacting spin chain. Its quantum version shows a quantum phase transition, from paramagnetic to ferromagnetic, at a critical value of the transverse field. Unlike thermodynamical phase transitions, this change of phase does not depend on temperature but on quantum fluctuations that occur at zero temperature. You can observe the phase transition by computing the expected value of magnetization.

However, it is possible to do even more interesting simulations using this particular circuit. As I said, this circuit maps the computational basis states to the Hamiltonian eigenstates, which means that we have access to the whole spectrum and not only the ground state. Using this property, we can simulate the time evolution of some observable, e.g. magnetization, as the characterization of all eigenstates is needed. As an example, I simulated the time evolution of the |0000> state magnetization: time variable is simply codified in a phase during initial state preparation.

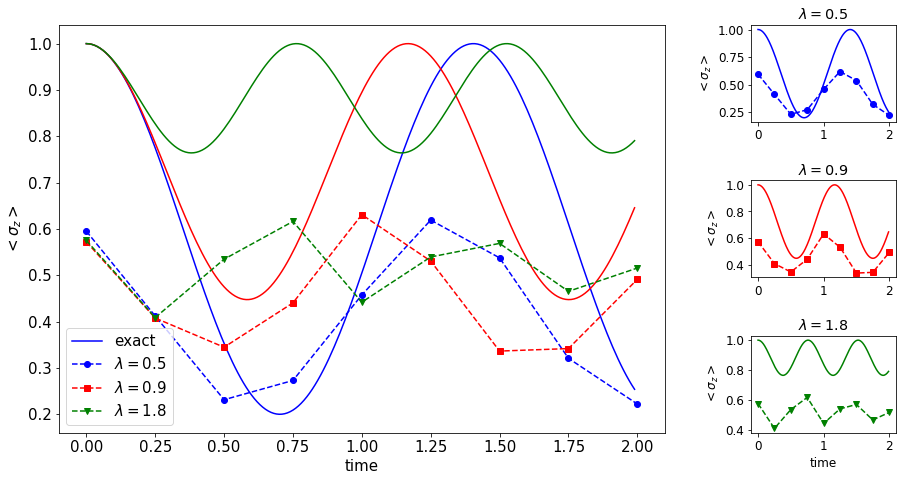
As the Ising model is integrable, it can be solved analytically, and the quantum circuit used can be generalized efficiently to a higher number of qubits. Then, this circuit can be used to benchmark quantum computers. All this work led to my first article written by my own.

While I was working on this project, IBM announced the IBM Q Awards, so I thought my work could be a good tutorial to learn how to use QISKit and an example of the applicability of quantum computation in condensed matter physics. Apparently judges thought the same, as they proposed my work as the winner. I could not be more honored for this recognition, even more after checking the incredible works from other people which are also available as QISKit tutorials.

We are living through an amazing period, witnessing the birth of a technology that involves the creation of a new paradigm in computation. In my opinion, the openning of the experiments and their programming tools to everybody not only democratizes science but also boosts its progress.