Quantum Computation: playing the quantum symphony

[Originally posted in Quantum World Association Medium page]

“A classical computation is like a solo voice — one line of pure tones succeeding each other. A quantum computation is like a symphony — many lines of tones interfering with one another.”― Seth Lloyd, Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos.

We adapt music to our feelings. An energetic rock track for our morning jog, some mellow tunes while reading a book at a cafe, or a soothing jazz for that unforgettable romantic dinner. There’s a song for every mood and occasion.

We adapt different types of computers to our needs and problems; there are numerous types of classical computers, each designed to solve specific problems (calculators to solve basic math operations, ebooks to read, mp4’s to listen to music, or supercomputers to solve intricate problems). Similarly, quantum computers will serve to solve specific types of problems, those that are out of reach for classical computers. Just like a smartphone is sufficient to check our emails, quantum processors won’t replace classical computers, but complement them. In the early development stages, quantum and classical algorithms will work in tandem, in a hybrid computational approach. Moreover, classical computers will be used to control/orchestrate the execution of quantum computations, as well as for essential pre- and post-processing tasks. Along these lines, the European Commission has assigned a team to create a bridge between the High-Performance Computing initiative (to build a world-class European supercomputing infrastructure) and the Quantum Technologies Flagship.

Let’s take a long breath now, because before we dive inside the quantum computing symphony, we should learn how quantum mechanics plays music.

The quantum tone: Qubit

The bit is the basic unit of information used in computation. It physically represents a two-state system, such as “on-off” or “open-closed”, and it is commonly labelled as either 0 or 1.

Do you remember the lovely music box? Ultimately, it’s an automatic machine, a kind of simplified computer, which produces sounds when the pin plucks the tuned teeth (in computational language, this could be a “1”) and does nothing if there is no pin when the teeth pass over (this could be the “0”). Then, we can describe this machine using bits by dividing it into sections, one for each musical note, and giving a string of 0’s and 1’s that tell us when the note is playing. The order of these strings of bits is given by the musical sheet and it’s very important! Otherwise, we can’t identify the song and it will probably sound dissonant. This is what we call an algorithm, a list of rules to follow in order to solve a problem (in this case, how to play a nice song). After that, the computer emits an output consisting of a string of bits, 0010110… (the musical notes) which encodes the solution (the song).

We are all familiar with music, but what if we want to construct a quantum music box? Then, all its components should obey the laws of quantum mechanics which, as you will see, are both very strange and useful.

The first thing to do is to have a quantum bit: the qubit. To differentiate it from a classical bit, a qubit is written between “|” and “>”. For example, |0> denotes a qubit in the logical state “0”. A string of qubits is written |0>|0>|1>|0>…, or for simplicity |0010…>. The first astonishing qubit characteristic, which has no equivalence in the world of classical bits, is that it could be in the state |0>, in the state |1> or in a superposition of both! For example, imagine that two possible configurations of a qubit correspond to two quantum-notes, for instance C and E (do and mi). Then we can construct a qubit state that we’ll call |♫>:

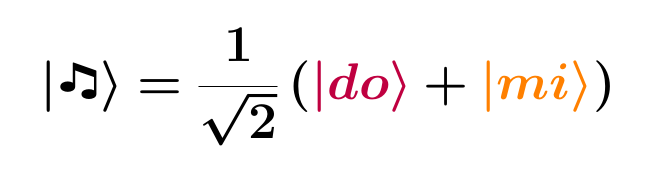
As we said, this has no equivalence in our world, the classical world. It only works in the quantum mechanical kingdom. But there is a way to extract information from that world: we can measure the qubit, listen to it. When we do that, we destroy the superposition, the state |♫> collapses and we force the qubit to reveal itself as either one state or the other: our quantum music box will play a |do> or a |mi>. If our box has thousands of |♫> states and we want to listen to them one by one, we will sometimes hear a |do>, sometimes a |mi>. The result after the measurement is probabilistic: in this example each note has 50% probability of being played.

Why is this useful? You might say “Ok, this is a very complicated way of describing a string of classical bits, as I can design a music box that reproduces the C note when the output is 0 and the E note when it’s 1 and make the result be probabilistic”. Of course you can! But then you cannot take advantage of the most important consequence of superposition: interference.

The quantum chords: Interference

If you have never played a piano before, and start pressing its keys randomly, it is very unlikely that you will produce a lovely melody. However, when Yuja Wang, a talented professional pianist, plays Mozart’s Turkish March the result is wonderful! The reason for that? She knows what keys to press, in what order, and with what intensity, not only because she knows the sheet; she also knows harmony and, therefore, how to combine individual sounds in order to obtain the desired melody.

Back to the quantum music box. Now that we have learnt how to construct such an object, we can start playing with it. We gained enough experience to create any quantum-tone, with different quantum notes and more sophisticated superpositions (with minus instead of plus, with other coefficients, etc). Imagine that at some point we put something — let’s call it H — between the quantum-teeth and the quantum-pins that make the |♫> tone change. By doing so, the |do> splits into a superposition of |do>+|mi> and the |mi> into |do>-|mi>: |♫> become a different tone, |♪>:

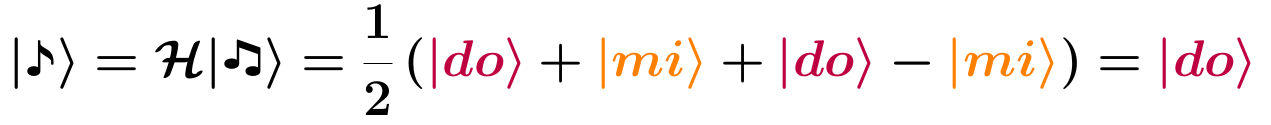
As a consequence, the two |mi> cancel each other due to quantum interference, and the final result is a lonely |do>: if we want to listen to |♪> we will always hear |do>. Herein lies the parallelism of quantum computing: we can modify the state with a single operation (H, a quantum gate) affecting the two quantum levels, |do> and |mi>, at the same time and in a different way.

Let’s continue with our qubit manipulation and let’s perform another quantum gate, U:

The qubit has changed completely since we started: now the probability of obtaining a |do> note is 80% and the probability of obtaining a |mi> is 20%.

What if we want to introduce more quantum notes? How can we construct a quantum-chord? Well, we can start playing with more than one qubit! Taking only two qubits, we can obtain a superposition of four notes, labelling |do> with |00>, |re> with |01>, |mi> with |10> and |fa> with |11>. With 3 qubits we can have all heptatonic quantum scale:

And so on and so forth. In general, with n qubits we can construct a superposition of 2^n states. Now imagine that we have a problem that involves n parties: we can assign one qubit/party, which allow us to explore a space of solutions of 2^n. Then, using quantum gates, we can operate with all qubits all together in a very clever way so the solutions that are not correct cancel each other because of quantum interference, just like H cancelled the |mi> note in our quantum music box. Or we can make the correct solution more probable to appear (amplitude amplification); by repeating the process many times we can guess what the true solution is, as the gate U did by increasing the probability of obtaining a |do>. Quantum algorithms exploit this strategy and enable us to solve problems using exponentially or polynomially fewer operations — depending on the problem — than a classical computer. The main example is the Shor’s algorithm, the one that is able to factorize prime numbers in a reasonable time meanwhile a supercomputer would take years. We will explain this problem in future entries for its importance in cryptography.

Classical computer cannot play a quantum symphony

Superposition is not the only perk that comes with quantum mechanics. Do you remember the birthday tale of the previous QWA entry? There, two twins shared a quantum entangled present, which consisted of a superposition of two cars and two pies. The twins would open their quantum presents each in their room. If one found a pie, she could not guess if it was due to randomness, or if her brother had opened his box before and collapsed the quantum present to a pie-pie. Entanglement is extraordinary. It was proven that highly entangled states cannot be described efficiently using classical physics (this is due to Bell’s theorem, an issue that we will cover in a future article). But entanglement is a property that naturally arises in quantum systems. Therefore, to study these systems and their characteristics, it will be crucial to use a quantum computer, which has the same properties, rather than a classical computer, which can — at best — approximate their description. This simple, but elegant thought, was the initial motivation that encouraged the Nobel Laureate Richard Feynman to theorize a quantum computer.

The quantum instruments and players

A quantum symphony requires quantum instruments, which can play with superpositions and entanglement. It’s a very novel kind of symphony, since constructions of these instruments has only begun in very recent years, and they are still under development and constant improvement. Just as the harpsichord evolved to the piano or the lyre to the violin, current quantum computers will allow for unprecedented computational tunes. Who will develop the quantum Stradivarius? Who is going to be the Stradivari that will build it? We have some candidates. The first company that launched a quantum computer was the Canadian DWAVE; it started in 2007 with a 16-qubit quantum annealing processor (an analog quantum computer) and its latest product contains 2000 qubits. Quantum annealers are also being developed by NNT in Japan and the startup Qilimanjaro. The giant computing company IBM was the first to offer a universal quantum computing processor (a digital quantum computer) on the cloud. Its first prototype was launched in 2016 and contained 5 qubits. One year later they launched a 16-qubit processor, and at the end of 2017 they made available a 20-qubit device and announced a 50-qubit one.

Other big computing multinational companies have also answered the quantum computing call. Google started with few-qubit quantum processors, and in March 2018 they announced a 72-qubit device. Microsoft is developing a quantum computer powered by a very special type of qubit, topological qubits; Nokia Bell Labs is pursuing the same strategy. Intel is building quantum chips currently being tested by QuTech group at Delft, the latest one a 49-qubit processor. Chinese tech giants have joined the race too: Alibaba has made an 11-qubit device, while Baidu is investing in its own quantum computing institute.

New companies are also betting on quantum computing. Rigetti was born as a startup from Y Combinator, and has raised USD$70 million from private investors: they have a 19-qubit device, which can be used on the cloud. Quantum Circuits Inc is also developing a superconducting quantum processor. Other new companies are betting for other kind of qubits than the superconducting qubits: IonQ is developing a quantum computer using ion qubits, Silicon Quantum Computing is developing a silicon based quantum integrated circuit and Xanadu a quantum photonic processor.

Besides quantum instruments, we need quantum composers and players: what kind of problems can we run on a quantum computer? How do we program and run these devices? Who can discover and develop algorithms? To answer these kind of questions, consulting, software and enabling technologies companies are emerging: Entanglement Partners and H-bar Quantum Consultants, both founders of QWA, are good examples. Major startups in the software space include 1Qbit, Zapata Computing and QxBranch. Early stage startups include Q-Ctrl, ProteinQure, Entropica Labs, Horizon Quantum, and the list is growing day by day!

QWA was born to connect everybody, players and composers, to create and play all together the most wonderful quantum symphony!

---

If you enjoyed this post, check other articles written by me and other members of the Quantum World Association! Check the QWA Medium page.